接合部温度TJの計算方法
熱抵抗
以下に、熱抵抗の概念図を示します。温度の規定位置は、パッケージや製品で異なります。
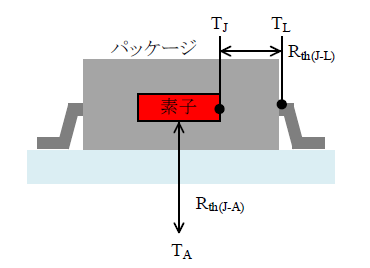
TJ:接合部温度
TL:リード温度
TA:周囲温度
Rth(J-L):接合部とリード間の熱抵抗
Rth(J-A):接合部と周囲間の熱抵抗
リード温度、周囲温度から計算する方法
ダイオードが動作しているときの損失と温度(リード温度TL、周囲温度TA)の実測値と、データシートの電気的特性に記載されている熱抵抗から接合部温度TJを推定します。TJは以下の式で計算できます。
- リード温度から推定した計算
- 周囲温度から推定した計算
| TJ = P × Rth(J-L) + TL |
| TJ = P × Rth(J-A) + TA |
ここで、
P:ダイオードの損失(W)
Rth(J-L):接合部とリード間の熱抵抗(°C/W)
Rth(J-A):接合部と周囲温度間の熱抵抗(°C/W)
TL:リード温度(°C)
TA:周囲温度(°C)
例として、P = 0.6 W、Rth(J-A) = 20 °C/W、TA = 80 °Cの場合、TJは以下の式で計算できます。
| TJ = 0.6 × 20 + 80 = 92 (°C) |
過渡熱抵抗特性から計算する方法
瞬間的に電力印加した際のTJは、過渡熱抵抗データから推定します。TJは以下の式で計算できます。
| TJ = P × rth(J-A) + TA |
ここで、
P:ダイオードの損失(W)
rth(J-A):接合部と周囲温度間の過渡熱抵抗(°C/W)
TA:周囲温度(°C)
以下に、SJPZ-N18の過渡熱抵抗特性を示します。例えば単発の矩形波100 msを印加した場合、rth(J-A) は9 °C/Wと読み取れます。
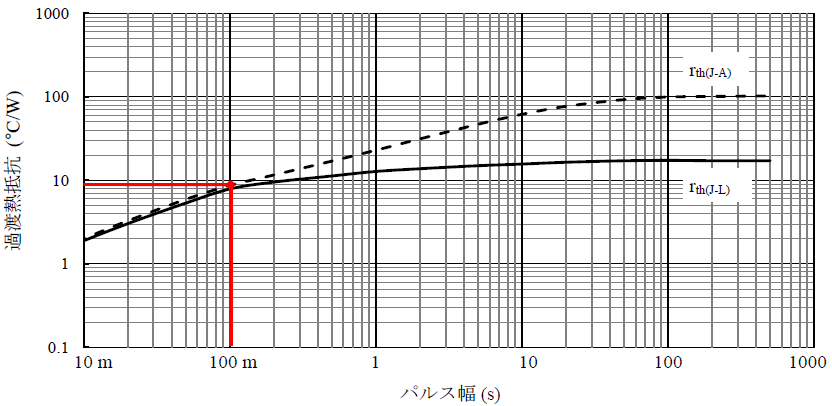
例えばP = 0.6 W、rth(J-A) = 9 °C/W、TA= 100 °Cの場合、TJは以下の式で計算できます。
| TJ = 0.6 × 9 + 100 = 105.4 (°C) |
重ね合わせの理を使用した計算方法
規則的な方形波の電力損失がダイオードに生じた場合と、不規則な方形波の電力損失がダイオードに生じた場合の接合部温度TJの算出方法を示します。このような電力損失波形の場合、各期間の熱抵抗をデータシートの過渡熱抵抗特性グラフから読み取り、重ね合わせの理を使用した算出方法が、容易で有効です。
連続パルス
(A)に示すように、規則的な方形波の電力損失がダイオードに生じた場合の接合部温度TJの算出方法を示します。全期間の平均電力損失に、2周期分の電力損失が発生したとする計算方法が容易です。
(B)と(C)に示すように、電力損失を近似し、重ね合わせの理を使用することでTJを算出します。

次に、(C)のブロックごとに、接合部温度を算出します。
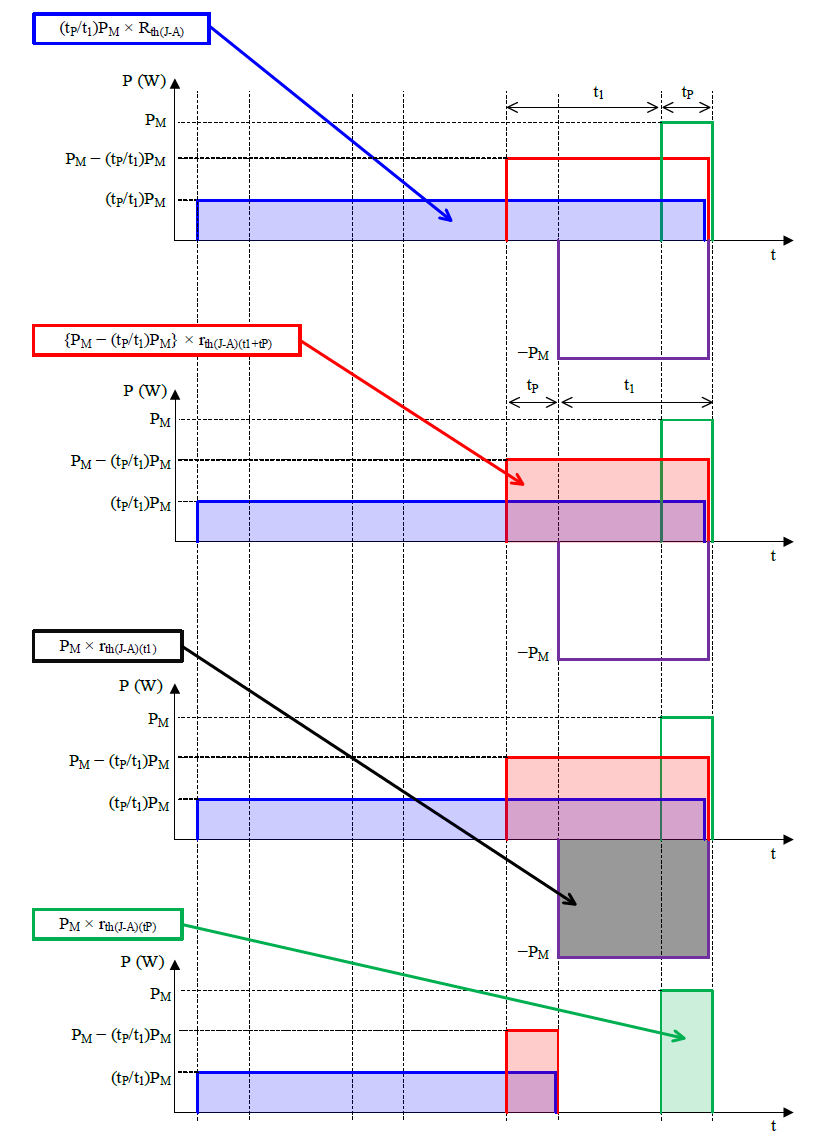
重ね合わせの理を使用した場合のTJは以下の式で計算できます。
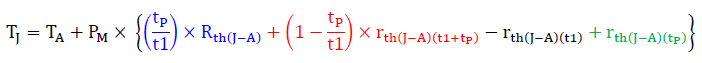 |
ここで、
TA:周囲温度(°C)
PM:平均電力損失(W)
t1:周期(s)
tP:パルス幅(s)
Rth(J-A):全期間の接合部と周囲温度間の熱抵抗(°C/W)
rth(J-A)(t1+tP):t1+tP期間の接合部と周囲温度間の熱抵抗(°C/W)
rth(J-A)(t1):t1期間の接合部と周囲温度間の熱抵抗(°C/W)
rth(J-A)(tP):tP期間の接合部と周囲温度間の熱抵抗(°C/W)
不規則パルス
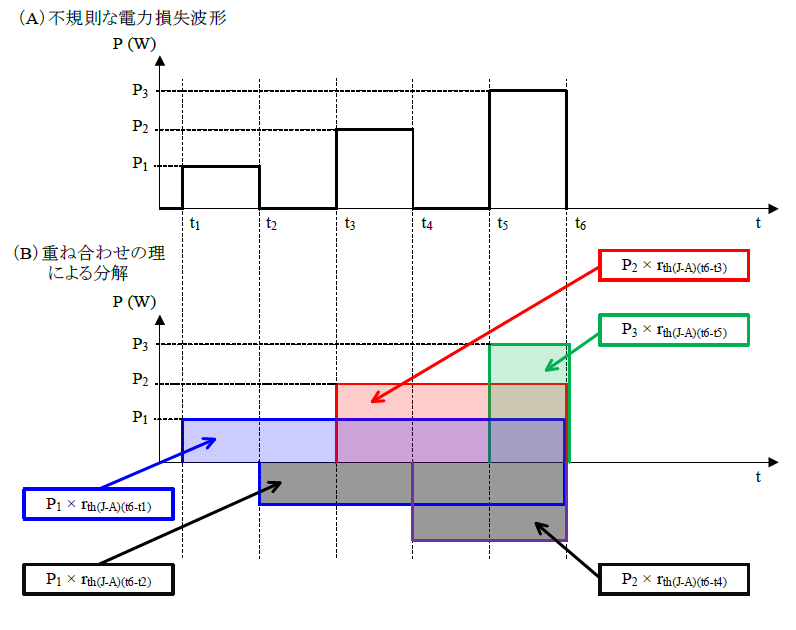
(A)に示すように、不規則な方形波の電力損失がダイオードに生じた場合の接合部温度TJの算出方法を示します。(B)に示すように、重ね合わせの理を使用し、ブロックごとの接合部温度TJを算出します。
よって、重ね合わせの理を使用した場合のTJは以下の式で計算できます。
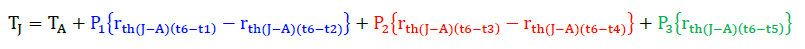 |
ここで、
TA:周囲温度(°C)
P1~P3:各パルスの電力損失(W)
rth(J-A)(t6−t1):t6−t1 期間の接合部と周囲温度間の熱抵抗(°C/W)
rth(J-A)(t6−t2):t6−t2 期間の接合部と周囲温度間の熱抵抗(°C/W)
rth(J-A)(t6−t3):t6−t3 期間の接合部と周囲温度間の熱抵抗(°C/W)
rth(J-A)(t6−t4):t6−t4 期間の接合部と周囲温度間の熱抵抗(°C/W)
rth(J-A)(t6−t5):t6−t5 期間の接合部と周囲温度間の熱抵抗(°C/W)
製品のお問い合わせやご相談はこちら
ご希望の製品がラインアップから見つからない場合もお気軽にお問い合わせください。
